surf

Plots a two-dimensional surface in ℝ³.

Syntax

• surf(equation[, urange, vrange[, color]])

  • equation is an equation

  • urange is a vector of the form ❨umin, umax[, udelta]❩

  • vrange is a vector of the form ❨vmin, vmax[, vdelta]❩

  • color is a colour-valued expression in x, y, and z

• surf([a, b[, δ]] × [c, d[, ε]] @ F)

  • a, b, and δ are real numbers

  • c, d, and ε are real numbers

  • F is a function [a, b] × [c, d] → ℝ³ or ℝ⁴

Description

The first syntax plots a surface specified by an equation in Cartesian coordinates.

If equation is a single equation in the Cartesian coordinates x, y, and z, with its LHS equal to one of those, and its RHS an expression containing only the other two coordinates, then surf(equation) plots the surface described by this equation. The independent variables vary from −10 to +10.

surf(equation, urange, vrange) plots the surface obtained as the first independent variable varies from umin to umax and the second variable varies from vmin to vmax, with steps udelta and vdelta, respectively. If the steps are omitted, default values are used.

surf(equation, urange, vrange, color) produces a coloured surface, where the colour at (x, y, z) on the surface is given by color. Without such an explicit colour function, the surface will be a single-colour surface.

The second syntax plots a parameterised surface.

Specifically, surf([a, b] × [c, d] @ F) plots the surface that is the image of the rectangular parameter-plane region D ≔ [a, b] × [c, d] ⊂ ℝ² under the map F: D → ℝ³.

If instead F: D → ℝ⁴, the last coordinate of F(u, v) is interpreted as the surface’s colour at that point.

δ and ε are the steps in the first and second parameter, respectively; if omitted, default values are used.

The object is shown in the current scene and a reference to the object is returned.

The AdjustVisual function can be used to adjust the appearance of the surface. See Visual settings for a list of applicable settings.

surface is a synonym of surf.

Examples

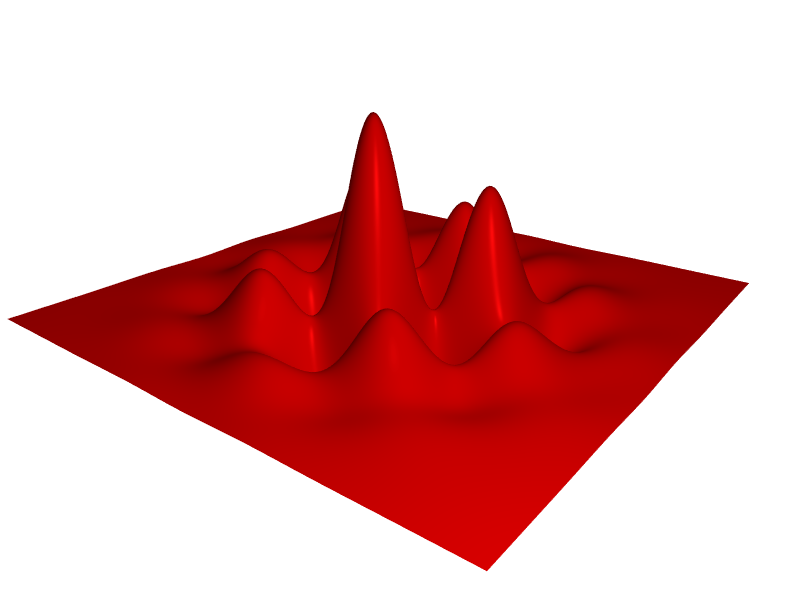
surf(z = sin(x^2/10 + y^2/10))

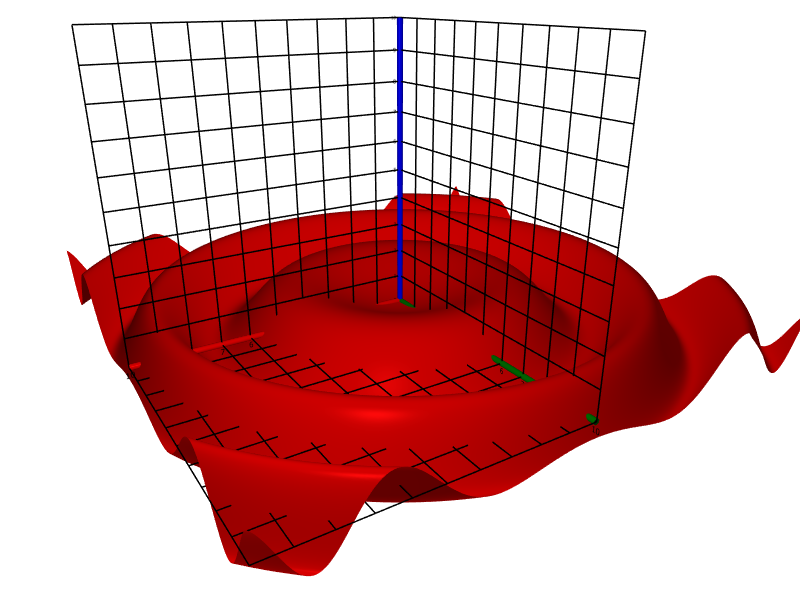
surf(z = 8⋅sin(x)⋅cos(y)⋅exp(−(x^2 + y^2)/20))

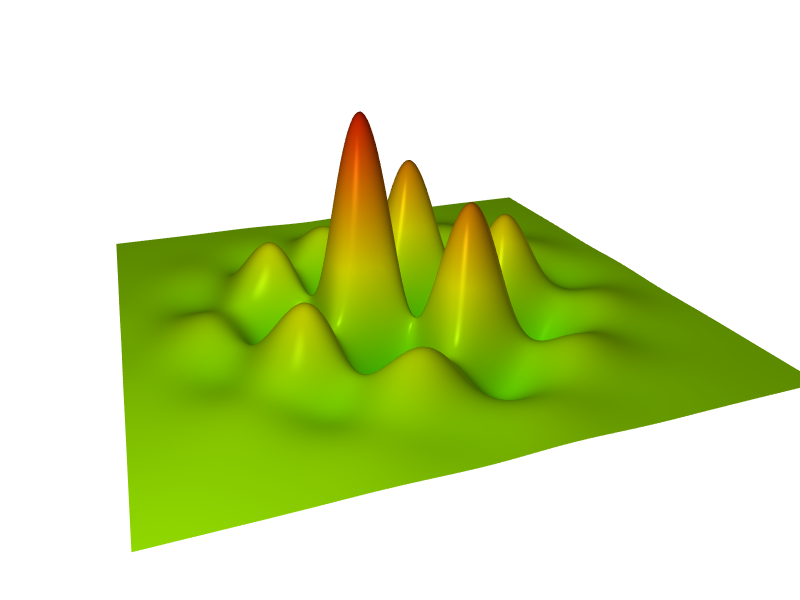
surf(z = 8⋅sin(x)⋅cos(y)⋅exp(−(x^2 + y^2)/20), ❨−10, 10❩, ❨−10, 10❩, hsv(10⋅(8 − z), 1.0, 1.0))

surf([0, π] × [0, 2⋅π] @ ((θ, φ) ↦ ❨sin(θ)⋅cos(φ), sin(θ)⋅sin(φ), cos(θ)❩));
AdjustVisual(ans, "show parameter curves": true)

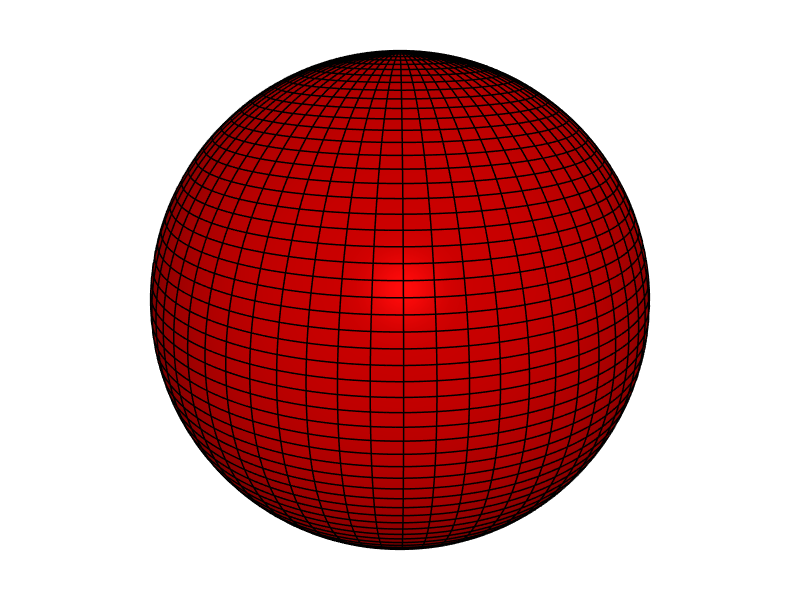
surf([−π, π] × [−π, π] @ ((θ, φ) ↦ ❨φ⋅sin(θ), φ⋅cos(θ), θ⋅cos(φ), integer(rgb((π+φ)/(2⋅π), (π+φ)/(2⋅π), (2⋅π+θ)/(3⋅π)))❩))

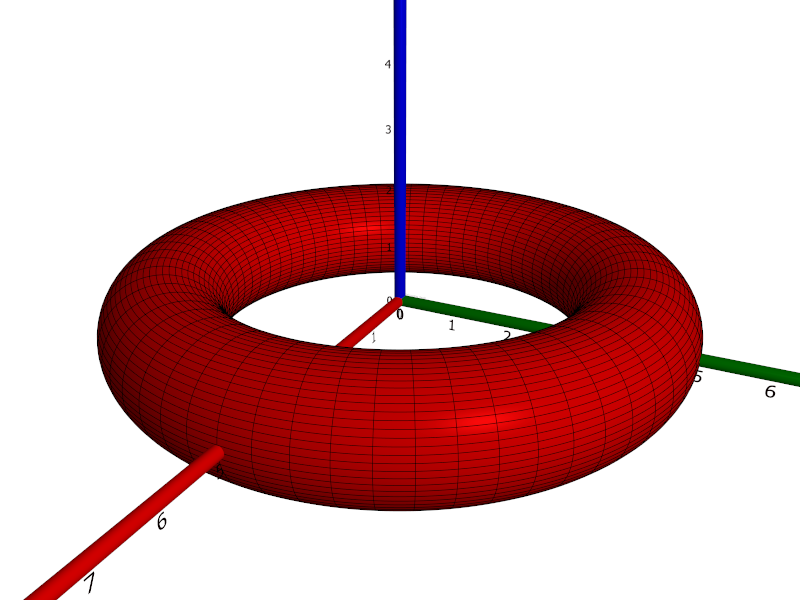
surf([0, 2⋅π] × [0, 2⋅π] @ ((u, v) ↦ ❨(4 + cos(v))⋅cos(u), (4 + cos(v))⋅sin(u), sin(v)❩));
AdjustVisual(ans, "show parameter curves": true)

See also

• curve

• plot