MovingAverage

Computes a moving average of a sequence of real or complex numbers.

Syntax

• MovingAverage(X[, n])

  • X is a vector, a list of numbers, a two-column matrix, or a list of (x, y) pairs

  • n is a positive integer

• MovingAverage(X, w)

  • X is a vector, a list of numbers, a two-column matrix, or a list of (x, y) pairs

  • w is a non-zero vector

Description

MovingAverage(X, n) computes the moving average of X with window size n, which defaults to 9 if not specified. In any case, n needs to be odd, so if n is even, the function will effectively use n + 1 as the window size instead.

If X is a vector of real or complex numbers, the result is a vector of the same type (but slightly reduced dimension) consisting of the moving average of X with window size n.

If X is a matrix of size m×2, the values of the first column of X are treated like data labels and the values of the second column as data values.

Hence, MovingAverage(X, n) returns a m′×2-sized matrix (with m′ slightly less than m) with the second column obtained from the original second column by computing the moving average of size n. For each row of the result, the label is the label of X for the value around which the output row average is centred.

If X is a list of numbers, MovingAverage(X, n) returns the list of moving averages of X with window size n.

If X is a list of vectors ❨x, y❩, the result is the list of moving averages of these data points with the x values treated like labels.

If omitted, n always defaults to 9.

MovingAverage(X, w) computes the moving average with relative weights w, a vector of numbers. w is used to describe the slope of the window from the centre point and outwards. The actual window used is obtained by joining two “copies” of w with the first one reversed and the central value at the joint only appearing once. Specifically, if the weight vector

w = ❨w1, w2, w3, ..., wk❩

then the window used for computing the moving average is the symmetric window

W = ❨wk, ..., w3, w2, w1, w2, w3, ..., wk❩

of size dim(W) = 2⋅k − 1 = 2⋅dim(w) − 1.

Although this behaviour of the MovingAverage function prevents the use of non-symmetric windows, it significantly simplifies the specification of symmetric windows.

In any case, the window is normalised before it is used to compute the moving average, so that ∑W = 1.

From the above discussion, it’s clear that

MovingAverage(X, 2⋅n − 1) = MovingAverage(X, ZeroVector(n) + 1)

where ZeroVector(n) + 1 is the vector of size n consisting of only ones. Also,

MovingAverage(X, t⋅w) = MovingAverage(X, w)

for any non-zero weight vector w and non-zero number t.

Examples

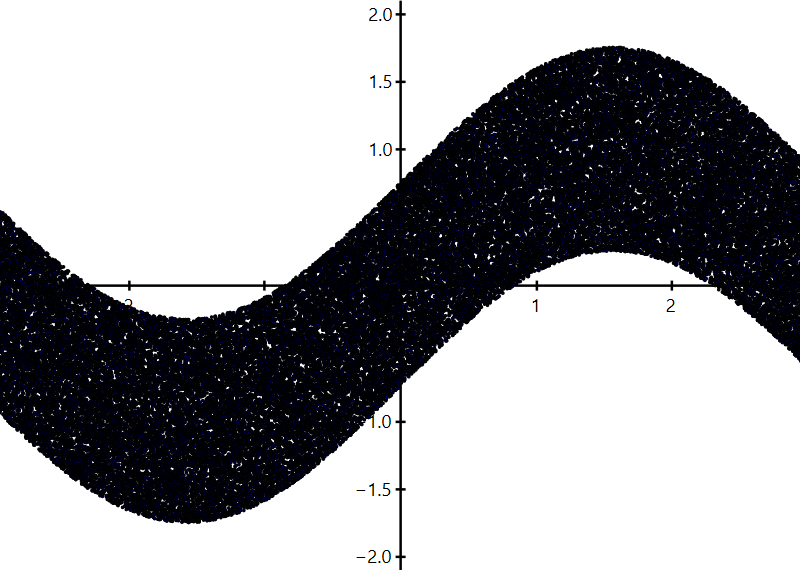
f ≔ x ↦ sin(x) + RandomReal(−.75, .75)

G ≔ graph(f, −π, π, 1e−4); plot(G)

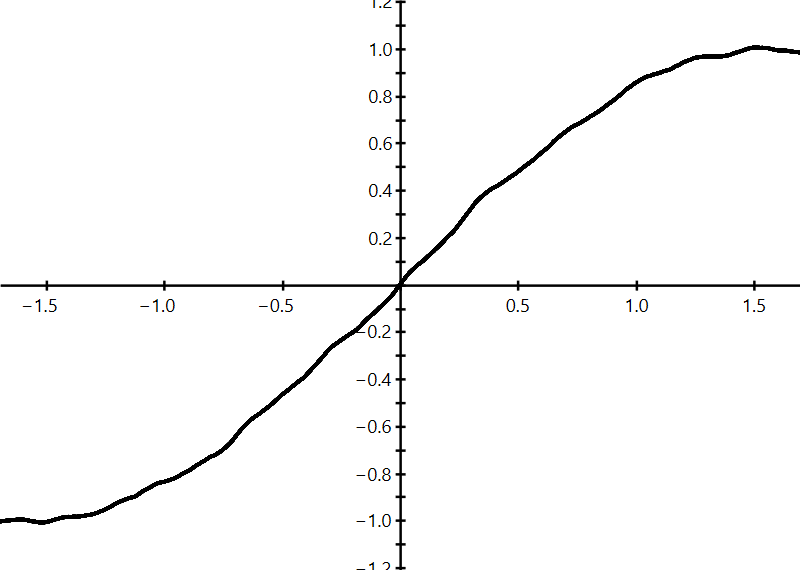
M ≔ MovingAverage(G, 1000); plot(M)

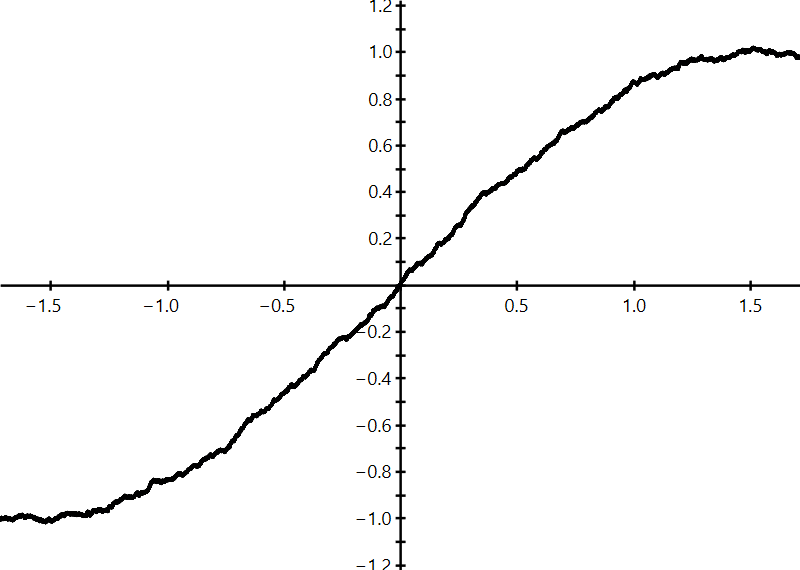
M ≔ MovingAverage(G, reverse(SequenceVector(1000))); plot(M)